2014.10.28掲載のリライト
有効数字の計算で重要な2つのこと
有効数字とは信頼できる数字のこと
有効数字をどこまで取るかはそれぞれの測定精度に関わってくる問題なので
それぞれの測定に対して有効数字を考える必要がある。
最終桁に誤差を含んでいる状態の値である
さて、これらを踏まえた上で「実際の計算ではどのように扱うのか?」ということが
知りたいポイントであろう。
結論から言うと
「和差は誤差の位の大きい所まで、乗除は有効数字の小さいものにそろえる」
が原則になります。
具体例
次の例を見ながら考えてみよう。
例1
$6.815+0.175-0.0836+15.49$
それぞれの値の有効数字は
$6.815$ ・・・ 4桁
$0.175$ ・・・ 3桁
$0.0836$ ・・・ 3桁
$15.49$ ・・・ 4桁
となっています。
この計算を筆算で表してみると
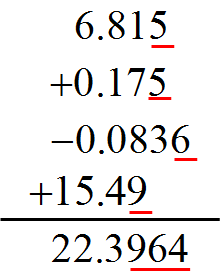
赤で下線が引いてある部分が誤差を含んでいる部分です。
これを見ると小数第2位の9まで誤差が含まれていることになります。
先ほど書いた「最終桁に誤差を含んでいる状態の値」という部分が重要で、
「最終桁以外に誤差が入っていてはいけない」という意味にもなります。
従って、小数第2位の9まで残すということになり、小数第3位を四捨五入にして$22.40$(有効数字4桁)となります。
つまり、$15.49$の$9$の部分が全体の有効数字を決定している状態になっていることがわかる。
例2
$12.61 \times 4.21$
それぞれの値の有効数字は
$12.61$ ・・・ 4桁
$4.21$ ・・・ 3桁
となっています。
この計算を筆算で表してみると
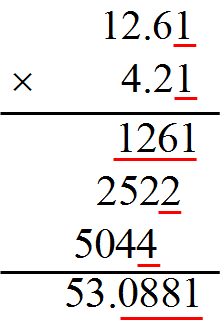
赤で下線が引いてある部分が誤差を含んでいる部分です。
これを見ると小数第1位の0まで誤差が含まれていることになります。
従って、小数第1位の0まで残すということになり、小数第2位を四捨五入にして$53.1$(有効数字3桁)となります。
つまり$4.21$の有効数字3桁にそろったことになっています。
有効数字の計算の考え方をまとめると
・有効数字は最終桁のみに誤差を含んでいる状態にすること
・よくわからなくなったら筆算で誤差の汚染がどこまで及んでいるかを確かめること
Keyword
物理学実験(experiment), 有効数字(significant figure)