2014.11.01掲載のリライト
自由落下の運動モデルで$v=gt, \ x=\frac{1}{2}gt^2$と表せる理由
自由落下の公式として知られている
\begin{eqnarray*}
v=gt, \ x=\frac{1}{2}gt^2
\end{eqnarray*}
を導いてみましょう。
力学の問題にあたる手順の通りやっていきましょう。
質量$m$の物体が自由落下しているモデル
手順1 ~ 軸を設定する
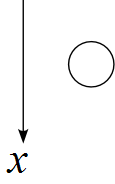
今回は下を正に設定しました。
別に上を正に設定して考えることもできます。
手順2 ~ 物体に作用している力を書く
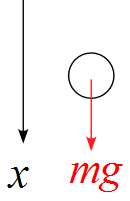
今回は空気抵抗は無いとすると作用している力は場の力である「重力$mg$」のみです。
手順3 ~ 運動方程式を立てる
\begin{eqnarray*}
ma=mg
\end{eqnarray*}
手順4 ~ 運動方程式を解く
\begin{eqnarray*}
ma &=& mg \\
m\frac{dv}{dt} &=& mg \\
\frac{dv}{dt} &=& g
\end{eqnarray*}
これを解くことになります。
両辺$t$で積分すると、
\begin{eqnarray*}
\int \frac{dv}{dt} dt &=&\int g\ dt \\
\int dv &=& \int g\ dt\\
v &=& gt+C
\end{eqnarray*}
となります。
不定積分なので積分定数$C$が出てくることを忘れないように。
この積分定数は初期条件により決定されます。
問題を解く場合は設定を確認しましょう。
今回の自由落下なので初速度が無いモデルなので$v(0)=0$となります。
この初期条件より
\begin{eqnarray*}
v(0)=g \cdot 0+C &=& 0 \\
C &=& 0
\end{eqnarray*}
よって速度$v(t)$は
\begin{eqnarray*}
v(t)=gt
\end{eqnarray*}
となるわけです。
続いて、速度から変位を求めます。
\begin{eqnarray*}
v(t)=\frac{dx}{dt} = gt
\end{eqnarray*}
両辺を$t$で積分して
\begin{eqnarray*}
\int \frac{dx}{dt} dt &=& \int gt \ dt\\
\int dx &=& \int gt\ dt\\
x &=& \frac{1}{2}gt^2 +C'
\end{eqnarray*}
$C'$は積分定数です。
係数の$\frac{1}{2}$は$t$を積分をしたときに出てきたものです。
ここで、初期条件を$t=0$のときを原点とすると
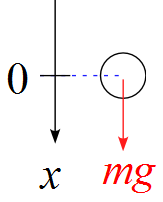
\begin{eqnarray*}
x(t) = \frac{1}{2} g \cdot 0^2 +C' &=& 0 \\
C' &=& 0
\end{eqnarray*}
よって
\begin{eqnarray*}
x(t) &=& \frac{1}{2} gt^2 \\
\end{eqnarray*}
となるわけです。
\begin{eqnarray*}
v(t) &=& gt\\
x(t) &=& \frac{1}{2} gt^2 \\
\end{eqnarray*}
と公式通りになっています。
面倒なことをしていると思いましたか?
今の説明は丁寧に書いたのでそう見えるかもしれませんが、
やっていることは
「運動方程式を立てて、$t$で積分して、初期条件を使った」
だけです。
グラフに表す
それぞれグラフに表すと
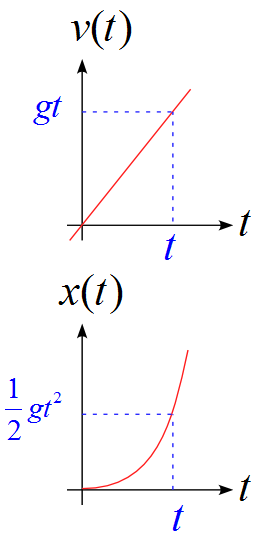
となります。
速度や変位はわかった。
じゃあ、エネルギーとかどうするのさ?
って話は次回にしましょう。