2014.11.11掲載のリライト
単位を考えることの重要性
学生実験中に「この量の単位は何ですか?」とよく聞かれます。
その度に「その量はどのようにして求めた物理量なのかを考えなさい。」と答えています。
求められた物理量は式の変形から導かれたものや、グラフの傾きから求められたものなどいろいろあります。
測定によって得られた測定値自身の場合もあります。
例えば、次のようなケースで傾きから物理量を求めたとします。
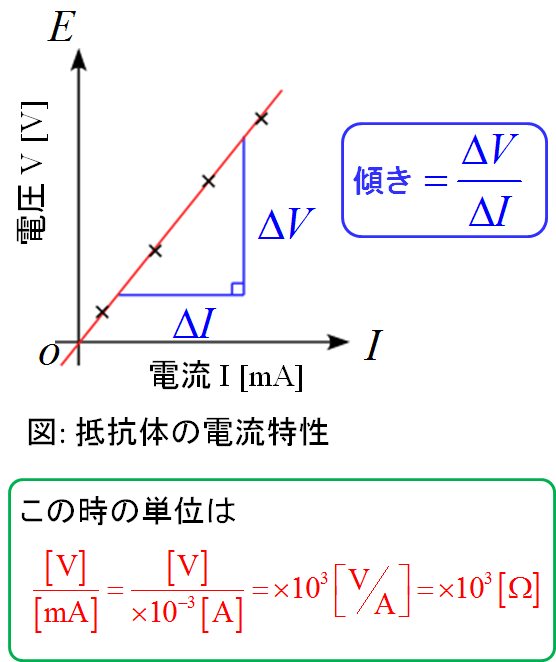
傾きを求めるとき、分母が電流$\ \mbox{I} \ $になり、分子が電圧$ \ \mbox{V}\ $になります。
グラフでの電流の単位は$\ [\ \mbox{mA} \ ]\ $なので、
SI系の単位にそろえる為、$\ \times 10^{-3} [\ \mbox{A} \ ]\ $と書き直します。
従って、$\ \times 10^{3} [\ \mbox{V/A} \ ]\ $となり、$\ \times 10^{3} [\ \Omega \ ]\ $と表せることになります。
この様に考えながら単位を決定します。
単位には物理的意味があります。
覚えるのではなく、その意味や構成要素を理解することが必要です。