2015.01.22掲載のリライト
等速度運動(等速直線運動)のモデル
物理の現象を考える時に2つのケースが考えられます。
抽象的な事象 → 具体的なモデル
具体的なモデル → 一般的な事象
今回は特殊なモデルである「等速度運動」について考えてみよう。
等速度な運動ということは「等しい速度」の運動ということである。
速度とは「速さと向き」を持った量である。
これが常に等しい運動であるため、別名「等速直線運動」と呼ばれています。
「向きが常に等しいならば、直線的に運動する」というわけです。
この等速直線運動は基本的なモデルと言うより、特殊なモデルと考えて頂きたい。
運動を理解するために簡単な条件に設定しているモデルです。
その点を踏まえて考えて行きましょう。
等速直線運動
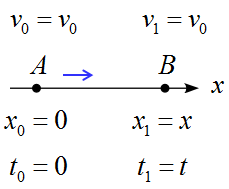
点Aの時、$x_0=0,\ t_0 =0,\ v_0=v_0\ $ とする。
(添え字の"$_0$"はスタート時という意味でゼロを振ってある。
さらに、簡単に考えるために点Aを原点とし、点Aを時刻ゼロに設定した。)
これが、点Bに来た時、$x_1=x,\ t_1 =t,\ v_1=v_0\ $となっていたとする。
(添え字の"$_1$"は1つ目の通過点という意味でイチと振ってある。)
速度が等しいので$v=v_0=v_1= const. $である。
(const. はconstant「定数・常数」の略である。ピリオドがある場合と無い場合がある。
大学ではこういった表記はよく使われます。)
A-B間の平均の速度を考えると、
$$
v=v_0=\frac{\Delta x}{\Delta t}=\frac{x_1-x_0}{t_1-t_0}=\frac{x-0}{t-0}=\frac{x}{t}
$$
と表すことができます。
この式を変形すると

となり、昔、算数で習ったような公式がでてきます。
当時の設定として、車や電車の速さ(速度)は一定というものでしたね。
ここで、この式$\ x=v_0 t\ $が示している意味について考えてみましょう。
等速直線運動について$v-t$グラフを書いてみると
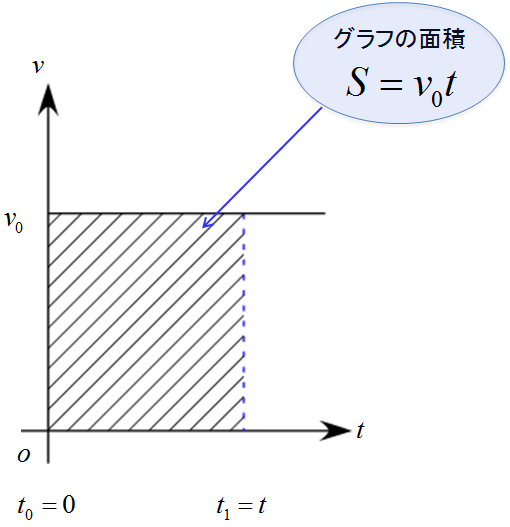
速度$v$が$v_0$で一定な運動なので、速度が常に$v_0$の直線になります。
ここで、この斜線で囲まれた部分の面積を考えると
$$
S= \mbox{縦} \times \mbox{横} = v_0 \times t =v_0 t
$$
と表すことができます。
さっきの変位$x $を表す式と同じものになっています。
これは偶然でしょうか?
等速度運動にだけ当てはまるのでしょうか?
それとも、一般的にも言えるのでしょうか?
ともかく、等速度運動の変位とv-tグラフの囲まれた部分の面積が等しいと言えそうです。
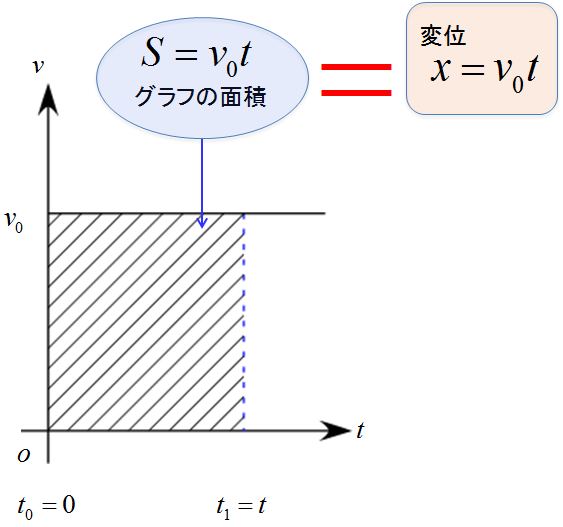
注)この、変位と$v-t$グラフの面積の関係は一般的に等しいと言えます。
詳細については後日掲載します。