2015.01.23掲載のリライト
等加速度運動
前回の等速度運動に引き続き、特殊なモデルである「等加速度運動」について考えてみよう。
次のようなモデルにおいて、
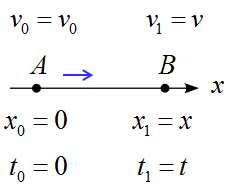
点Aの時、$x_0=0,\ t_0 =0,\ v_0=v_0\ $ とする。
これが、点Bに来た時、$x_1=x,\ t_1 =t,\ v_1=v\ $となっていたとする。
(簡単に考えるために点Aを原点とし、点Aを時刻ゼロに設定した。)
A-B間の平均の加速度を考えると、
$$
a=\frac{\Delta v}{\Delta t}=\frac{v_1 - v_0}{t_1 -t_0 }=\frac{v-v_0}{t-0}=\frac{v-v_0}{t}
$$
従って
$$
a=\frac{v-v_0}{t}
$$
と表すことができます。
この式を変形すると
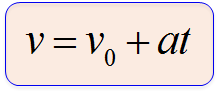
となります。
ここで、$v-t$グラフを書いてみると
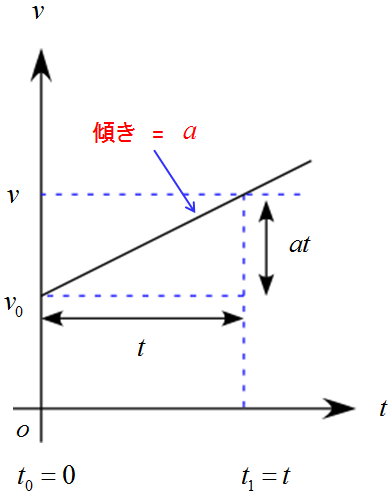
速度はスタート時、$v_0$で一定の割合で増加していく。つまり、等しい加速ということを表している。

この囲まれた部分の面積を考えると
$$
S=①+②=v_0 t +\frac{1}{2}at^2
$$
となります。
等速度運動の時と同じように考えれば、この面積が変位$x$になります。
等加速度運動でわかったことは
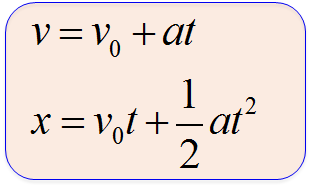
となります。
さて、「何故$v-t$グラフの囲まれた面積が変位になるのか?」について
次回に説明したいと思います。