2015.01.29掲載のリライト
等加速度運動の変位と$v-t$グラフの囲まれた面積
前回に引き続き「等加速度運動」のモデルです。
次のようなモデルにおいて、
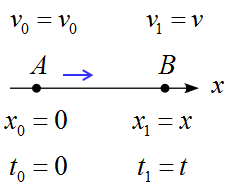
点Aの時、$x_0=0,\ t_0 =0,\ v_0=v_0\ $ とする。
これが、点Bに来た時、$x_1=x,\ t_1 =t,\ v_1=v\ $となっていたとする。
(簡単に考えるために点Aを原点とし、点Aを時刻ゼロに設定した。)
この等加速度運動において、平均の速度を考えることにより、変位を求めてみよう。
平均の速度は
$$
\bar{v}=\frac{\Delta x}{\Delta t}=\frac{x_1 - x_0}{t_1 -t_0 }=\frac{x-0}{t-0}=\frac{x}{t}
$$
であるから、変位$x$は
$$
x=\bar{v}\times t
$$
と表される。
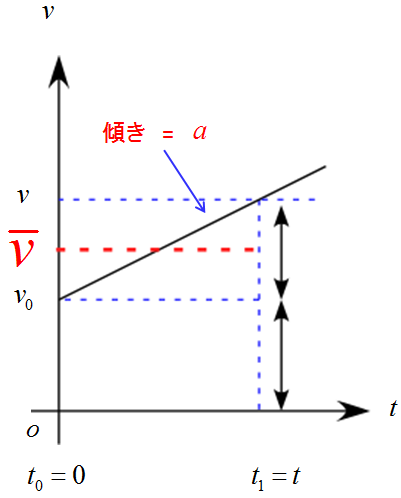
加速度$a$が一定な運動なので、$v(t)$は直線で表されている。
よって、平均の速度$\bar{v}$は
$$
\bar{v}=\frac{1}{2}(v+v_0)
$$
と表すことができる。
よって変位$x$は
\begin{eqnarray*}
x&=&\bar{v}\cdot t \\
&=& \frac{1}{2}(v+v_0) t \\
&=& \frac{1}{2} (v_0 +at +v_0)t \\
&=& \frac{1}{2} (2v_0 +at) t \\
&=& v_0t+\frac{1}{2} at^2
\end{eqnarray*}
となり、前回に求めた面積$S$と一致する。
グラフから考えると、
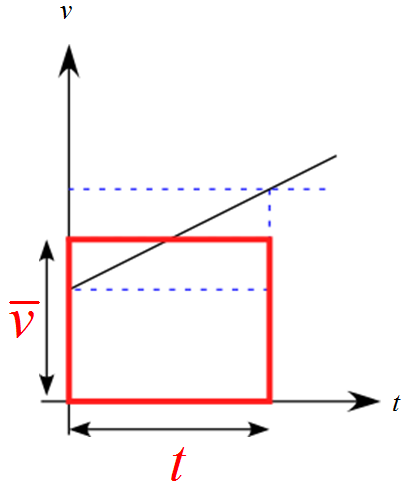
上図の赤で囲まれた部分の面積を求めたことに相当します。
等加速度運動でもv-tグラフで囲まれた面積を求めることは
変位を求めることと同じと言えます。
前回提示した変位$x$の式は正しいと言えます。
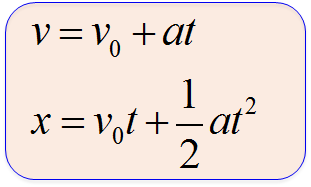
次回は、一般的な話をしたいと思います。