2015.01.21掲載のリライト
加速度~定義
前回、速度の定義について考えた。
速度の定義は
$$
v=\frac{dx}{dt}
$$
で表される。
変位$x$の時間変化率ということである。
この速度の時間に対する変化率を考えたものが加速度である。
つまり、「どれくらいの時間をかけて、どれくらい速度が変化するか」の度合いを考えることである。
これについて次のモデルを用いて考えてみよう。
平均の加速度
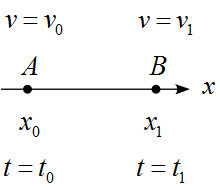
$t=t_0$で$x_0$の位置(点A)にある物体が移動して、$t=t_1$で$x_1$の位置(点B)にあったとする。
$t=t_0$の時の速度は$v_0$で、$t=t_1$では速度$v_1$になったとする。
この変化を$v-t$グラフで表すと次のようになります。
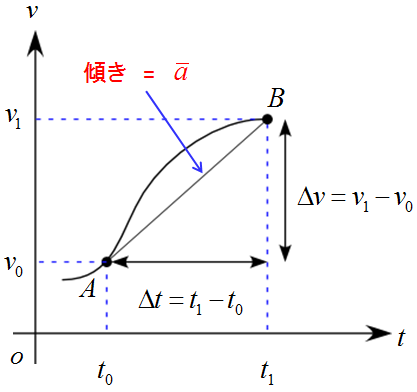
この運動では、$\Delta t =t_1-t_0$ の間に速度が$\Delta v =v_1-v_0$ だけ変化したことになります。
この変化率$\frac{\Delta v}{\Delta t}$ が平均の加速度$\bar{a}$になります。
点Aを出発して点Bまで移動していく間の加速度はどうなっているかは判らない。
加速度が大きい時間帯もあれば、あまり加速しない時間帯もある。
全体を平均して考えて平均の加速度とします。
$$
平均の加速度\ \bar{a}=\frac{\Delta v}{\Delta t}=\frac{v_1-v_0}{t_1-t_0}
$$
瞬間の加速度
平均の加速度がわかったら、今度はある瞬間の加速度を考えてみましょう。
考え方は基本的に同じです。
モデルで考えてみましょう。
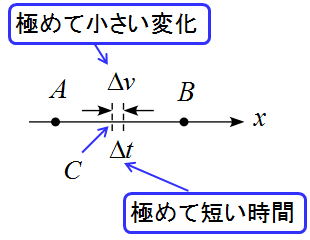
この変化を$v-t$グラフで表すと次のようになります。
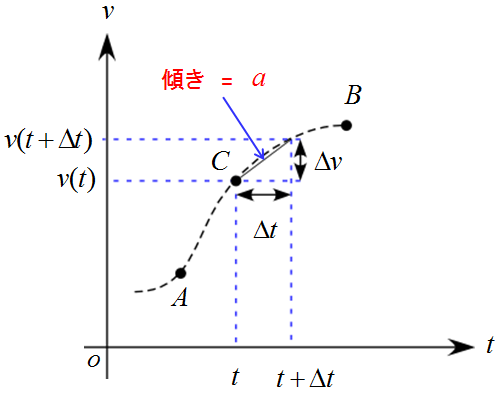
考え方は速度の時と同じく、$\Delta t \to 0$ の極限を考えることになります。
瞬間の加速度は
$$
a=\lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t}=\lim_{\Delta t \to 0} \frac{v(t+\Delta t)-v(t)}{\Delta t}=\frac{dv}{dt}
$$
これが加速度の定義になります。
加速度の定義
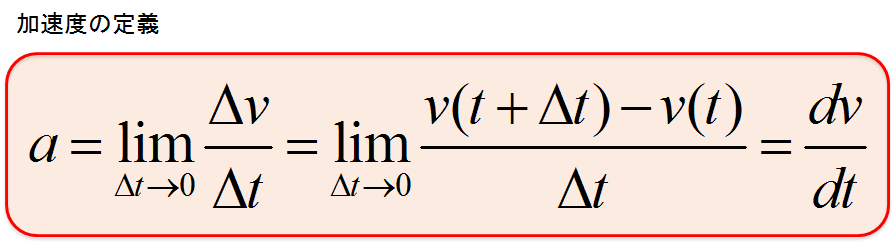
即ち、
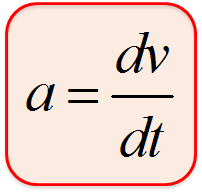
となります。
ここで、変位、速度、加速度の関係式が揃いました。
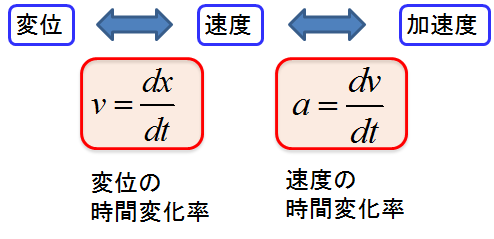
これらの関係式から変位から加速度を求めたり、
加速度から変位を求めたりすることができます。