2014.10.30掲載のリライト
$f(x)=x^n\ $を$\ x\ $で微分すると$\ nx^{n-1}\ $となる理由
微分の計算をやったことがある人であれば「最初に覚えるであろう公式」である。
「何故、肩の$n$が前に出てきて、肩が$n-1$になるのか考えたことはありますか? 」
普段、計算をする場合は公式を使うだけで良いのですが、「何故?」を考え理解しておく事は重要です。
この公式を微分の定義から導出してみましょう。
微分の定義
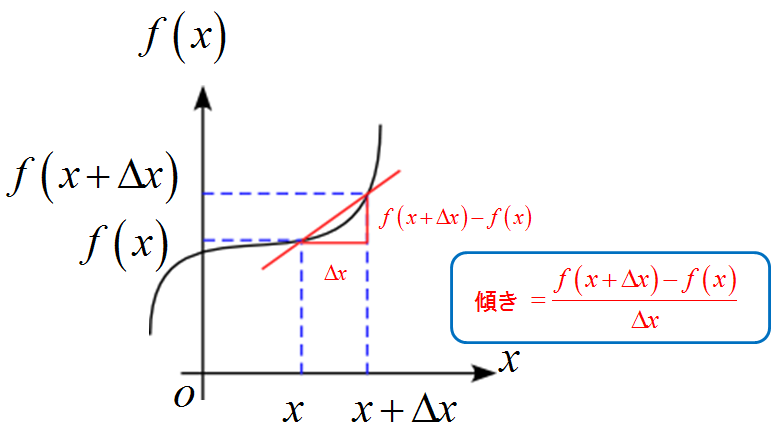
微分の定義は
$$
f'(x)=\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}
$$
であるから、
$$
\frac{df(x)}{dx}=\lim_{\Delta x \to 0} \frac{(x+\Delta x)^n -x^n}{\Delta x}
$$
この式を計算することになるわけです。
$n=1$の時
\begin{eqnarray*}
\frac{df^1(x)}{dx} &=& \lim_{\Delta x \to 0} \frac{(x+\Delta x)^1 -x^1}{\Delta x} \\
&=& \lim_{\Delta x \to 0} \frac{x+\Delta x -x}{\Delta x} \\
&=& \lim_{\Delta x \to 0} \frac{\Delta x}{\Delta x} \\
& & \\
&=& 1
\end{eqnarray*}
であり、
\begin{eqnarray*}
\frac{df^1(x)}{dx} &=& \frac{d}{dx} (x^1) = 1 \cdot x^{(1-1)} = 1 \cdot x^0 = 1\\
\end{eqnarray*}
と一致しています。
$n=2$の時
\begin{eqnarray*}
\frac{df^2(x)}{dx} &=&
\lim_{\Delta x \to 0} \frac{(x+\Delta x)^2 -x^2}{\Delta x} \\
&=&
\lim_{\Delta x \to 0} \frac{x^2 +2x\Delta x + \Delta x^2 -x^2}{\Delta x} \\
&=&
\lim_{\Delta x \to 0} \frac{2x\Delta x + \Delta x^2}{\Delta x} \\
&=&
\lim_{\Delta x \to 0} (2x + \Delta x)\\
& & \\
&=& 2x
\end{eqnarray*}
であり、
\begin{eqnarray*}
\frac{df^2(x)}{dx} &=& \frac{d}{dx} (x^2) = 2 \cdot x^{(2-1)} = 2 \cdot x^1 = 2x\\
\end{eqnarray*}
と一致しています。
$n=3$の時
\begin{eqnarray*}
\frac{df^3(x)}{dx} &=&
\lim_{\Delta x \to 0} \frac{(x+\Delta x)^3 -x^3}{\Delta x} \\
&=&
\lim_{\Delta x \to 0} \frac{x^3 +3x^2 \Delta x + 3x \Delta x^2 + \Delta x^3 -x^3}{\Delta x} \\
&=&
\lim_{\Delta x \to 0} \frac{3x^2 \Delta x + 3x \Delta x^2 + \Delta x^3}{\Delta x} \\
&=&
\lim_{\Delta x \to 0} (3x^2 + 3x \Delta x + \Delta x^2) \\
& & \\
&=& 3x^2
\end{eqnarray*}
であり、
\begin{eqnarray*}
\frac{df^3(x)}{dx} &=& \frac{d}{dx} (x^3) = 3 \cdot x^{(3-1)} = 3 \cdot x^2 = 3x^2\\
\end{eqnarray*}
と一致しています。
ここまでの計算を見てみると、
$f(x+\Delta x)$において
$x^n$の項は$f(x)$である$x^n$と相殺して無くなる。
$\Delta x$が1次の項は分母の$\Delta x$と約分になって$nx^{n-1}$が残る。
$\Delta x$が2次の項は分母の$\Delta x$と約分になって$\Delta x$の1次以上が残る。
この項は$\Delta x \to 0$の極限では$0$に収束する。
従って、$\Delta x$が1次の項のみ残ることになる。
ということは
$(x+\Delta x)^n$の展開において$\Delta x$の1次の項のみ考えれば良いことになる。
この展開は2項定理と呼ばれる法則がある。
この話はまた別の機会でしましょう。
実際に計算してみると
となります。
どのような経緯になっているのかが理解できるとスッキリできます。
