2014.11.05掲載のリライト
上向きを正に軸を取った場合の自由落下
別に軸は自由に取っていいので場合分けなんてする必要はないのですが、
実感をしてもらうために一応やってみましょう。
手順1 ~ 軸を設定する
軸を上にとって、
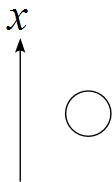
手順2 ~ 物体に作用する力を書く
作用する力を書き込みます。
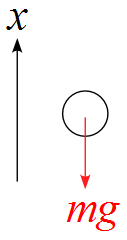
今回は空気抵抗は無いとすると作用している力は場の力である「重力$mg$」のみです。
手順3 ~ 運動方程式を立てる
運動方程式を立てます。
\begin{eqnarray*}
ma=-mg
\end{eqnarray*}
上向きを正にしているのに対して重力$mg$は下向きです。
従って、$-mg$とします。
手順4 ~ 運動方程式を解く
\begin{eqnarray*}
ma &=& -mg \\
m\frac{dv}{dt} &=& -mg \\
\frac{dv}{dt} &=& -g
\end{eqnarray*}
これを解くことになります。
両辺$t$で積分すると、
\begin{eqnarray*}
\int \frac{dv}{dt} dt &=& -\int g\ dt \\
\int dv &=& - \int g\ dt\\
v &=& -gt+C
\end{eqnarray*}
となります。
不定積分なので積分定数$C$が出てくることを忘れないように。
この積分定数は初期条件により決定されます。
問題を解く場合は設定を確認しましょう。
今回の自由落下なので初速度が無いモデルなので$v(0)=0$となります。
この初期条件より
\begin{eqnarray*}
v(0)=-g \cdot 0+C &=& 0 \\
C &=& 0
\end{eqnarray*}
よって速度$v(t)$は
\begin{eqnarray*}
v(t)=-gt
\end{eqnarray*}
となるわけです。
続いて、速度から変位を求めます。
\begin{eqnarray*}
v(t)=\frac{dx}{dt} =- gt
\end{eqnarray*}
両辺を$t$で積分して
\begin{eqnarray*}
\int \frac{dx}{dt} dt &=& - \int gt \ dt\\
\int dx &=& -\int gt\ dt\\
x &=& -\frac{1}{2}gt^2 +C'
\end{eqnarray*}
$C'$は積分定数です。
係数の$\frac{1}{2}$は$t$を積分をしたときに出てきたものです。
ここで、初期条件を$t=0$のときを原点とすると
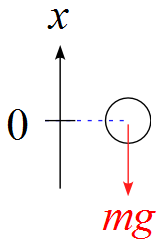
\begin{eqnarray*}
x(t) =- \frac{1}{2} g \cdot 0^2 +C' &=& 0 \\
C' &=& 0
\end{eqnarray*}
よって
\begin{eqnarray*}
x(t) &=& -\frac{1}{2} gt^2 \\
\end{eqnarray*}
となるわけです。
従って、
\begin{eqnarray*}
v(t) &=& -gt\\
x(t) &=& -\frac{1}{2} gt^2 \\
\end{eqnarray*}
となります。
この$-$(マイナス)の意味は上向きを正に軸を取った時、
速度$v$や変位$x$はその逆向きであることを示しています。
グラフに表す
それぞれグラフに表すと
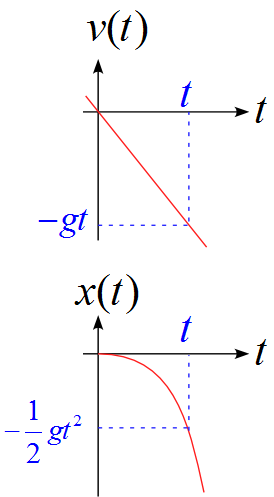
となります。
軸の取り方って重要だと思いませんか?
公式として暗記をする前に、その成り立ちを理解しておけば
「符号がどっちだっけ?」なんて間違いはありません。
軸をどのように取るかで符号が変わります。
その符号は何を意味しているのか?を考えることが大事ですよ。