2014.11.02掲載のリライト
自由落下の運動モデルにおける仕事とエネルギーの関係
運動方程式の検討
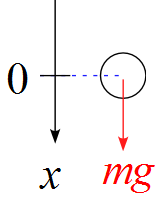
さて、まずは運動方程式に戻って考えます。
下を正に取った場合の自由落下の運動方程式は、
\begin{eqnarray*}
ma &=& mg \\
m\frac{dv}{dt} &=& mg \\
\end{eqnarray*}
と書くことができます。
この運動方程式の両辺に$v=\frac{dx}{dt}$をかけると
\begin{eqnarray*}
m\frac{dv}{dt}v &=& mg \frac{dx}{dt} \\
\frac{d}{dt} \Bigl( \frac{1}{2}mv^2 \Bigr) &=& \frac{d}{dt} \Bigl( mgx \Bigr)
\end{eqnarray*}
となります。
この式を見ると、
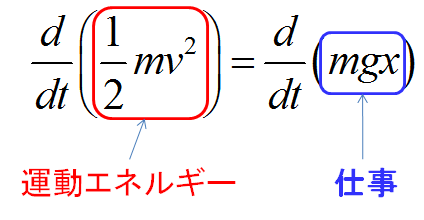
$\frac{1}{2}mv^2$の部分を運動エネルギー、$mgx$を仕事と呼びます。
つまり、この運動方程式(自由落下)は

ということを表しています。
さらに、
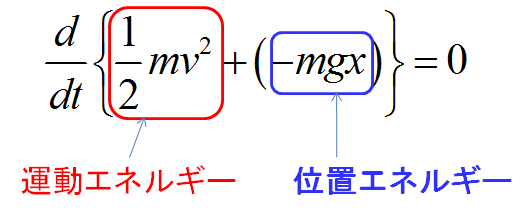
と表すことができます。
注) 右辺にある場合「仕事」と呼び、左辺に来ると同じものを「エネルギー」と呼びます。
さて、この式は、
「運動エネルギー」と「位置エネルギー」の和の「変化量がゼロ」
と言うことを表しています。
「運動エネルギー」と「位置エネルギー」の和を「力学的エネルギー」と呼びます。
この「力学的エネルギーの変化量」が「ゼロ」になっているので、
「力学的エネルギーが保存している」と言えます。
所謂、「(力学的)エネルギー保存則」というものです。
自由落下のモデルにおいて、エネルギー保存則が成り立っていることが言えるのは、
運動方程式から言えることなのです。
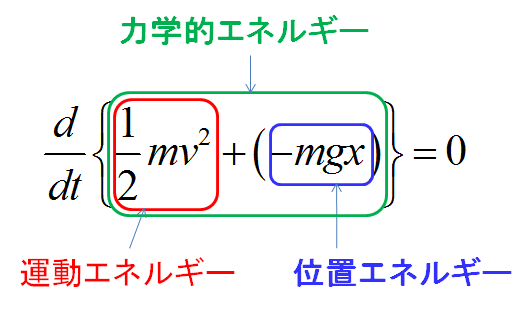
ここで、
\begin{eqnarray*}
\frac{d}{dt} \Bigl\{ \frac{1}{2}mv^2 + \Bigl(- mgx \Bigr) \Bigr\} = 0
\end{eqnarray*}
この式に前回導いた、
\begin{eqnarray*}
v(t) &=& gt\\
x(t) &=& \frac{1}{2} gt^2 \\
\end{eqnarray*}
を代入してみましょう。
\begin{eqnarray*}
\frac{d}{dt} \Bigl\{ \frac{1}{2}mv^2 + \Bigl(- mgx \Bigr) \Bigr\} & & \\
\frac{d}{dt} \Bigl\{ \frac{1}{2}m\ (gt)^2 + \Bigl(- mg\ \Bigl(\frac{1}{2}gt \Bigr) \Bigr) \Bigr\} & & \\
\frac{d}{dt} \Bigl\{ \frac{1}{2}m\ g^2t^2 - \frac{1}{2} m g ^2 t^2 \Bigr\} &=& 0
\end{eqnarray*}
となります。
現象を定性的に考えてみましょう。
落下していくにつれて速度$v(t)$は速くなり、運動エネルギー$K(t)$も大きくなります。
一方、落下すると変位$x(t)$は大きくなるが、下向きを正に軸を取っているので、位置エネルギー$U(t)$は小さくなっていきます。
その2つが合わさると、ちょうど「ゼロ」になっていると考えられます。
E-tグラフ
運動エネルギー$K(t)$と位置エネルギー$U(t)$、及び力学的エネルギー$E(t)$をグラフに表すと
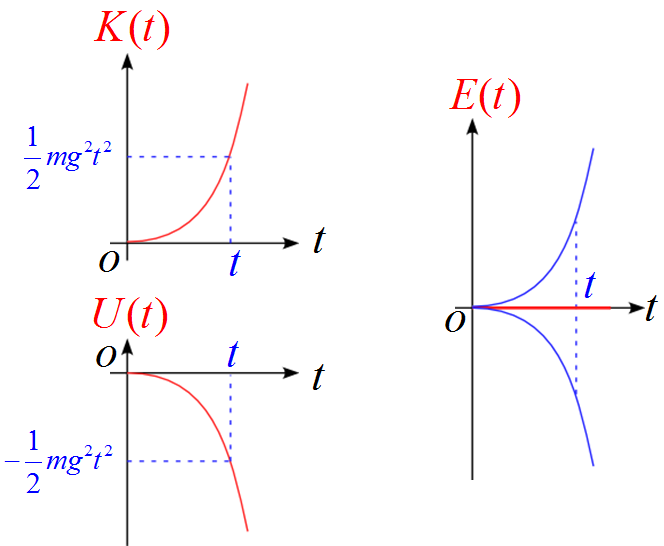
となります。
どうでしたか?
力学(ニュートン力学)の基本は運動方程式です。
運動方程式を正しく立てることができ、理解することが重要なのです。