2015.01.05掲載のリライト
速度〜定義
物体の位置が変化したとき変位で表す。
この変位の変化が時間的にどれくらいか?が知りたい。
ゆっくりと変化したのか、
すばやく変化したのかは興味深いことである。
物理学において時間変化は非常に重要な事である。
平均の速度
この位置の変化=変位が時間的にどうなっているのかを
モデルを使って考えてみることにしよう。
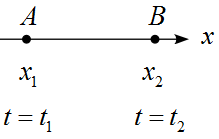
$t=t_1$で$x_1$の位置(点A)にある物体が移動して、$t=t_2$で$x_2$の位置(点B)にあったとする。
この変化を$x-t$グラフで表すと次のようになります。
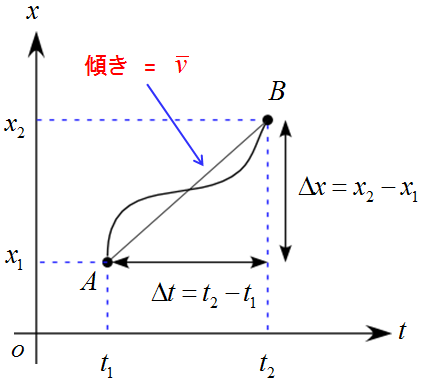
この運動では、$\Delta t =t_2-t_1$の間に$\Delta x =x_2-x_1$だけ変位したことになります。
この変化率$\frac{\Delta x}{\Delta t}$が平均の速度$\bar{v}$になります。
点Aを出発して点Bまで移動していく間の速度はどうなっているかは判らない。
速く変位する時間帯もあれば、ゆっくり変位する時間もあるが、
全体を平均して考えて平均の速度とします。
$$
平均の速度\ \bar{v}=\frac{\Delta x}{\Delta t}=\frac{x_2-x_1}{t_2-t_1}
$$
瞬間の速度
平均の速度がわかったら、今度はある瞬間の速度が知りたくなりますよね?
考え方は基本的に同じです。
モデルで考えてみましょう。
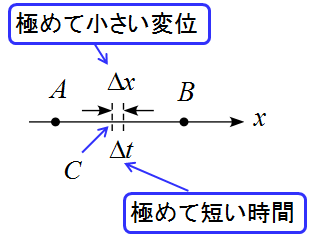
点Aから点Bに変位する途中において点Cを設定します。
この点Cでの速度を考えることにします。
この変化を$x-t$グラフで表すと次のようになります。
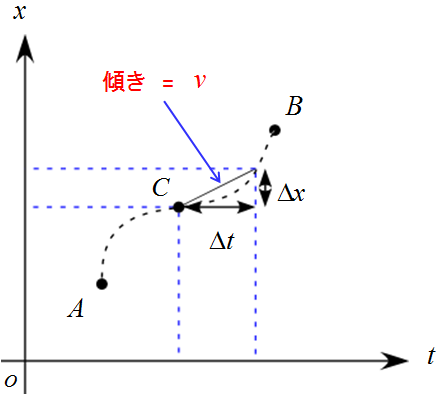
$\Delta t$や$\Delta x$は極めて小さいと考えて下さい。
それでも、点Cでの速度にはなりません。
$\Delta t$をもっと短くする必要があります。
即ち$\Delta t \to 0$の極限を考えます。
拡大をしていくイメージです。
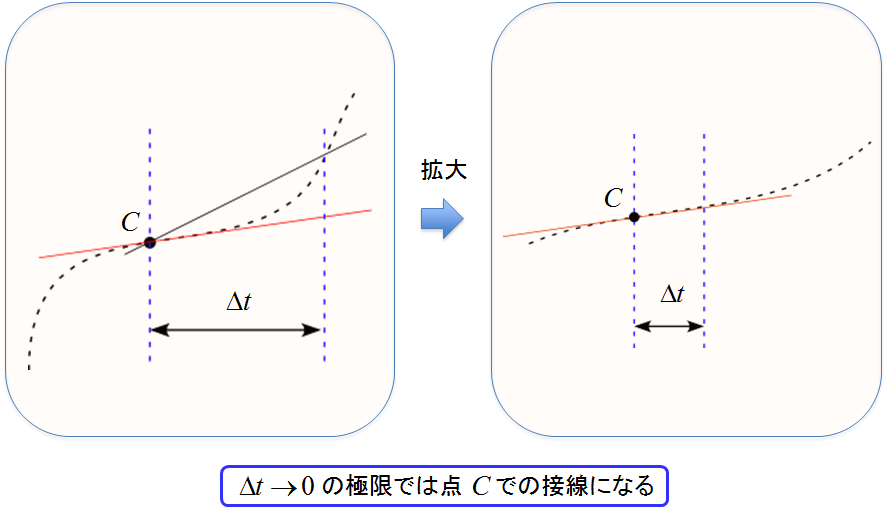
点Cの時刻を$t$とすると
従って、瞬間の速度は
$$
v=\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t}=\lim_{\Delta t \to 0} \frac{x(t+\Delta t)-x(t)}{\Delta t}=\frac{dx}{dt}
$$
これが速度の定義になります。
速度の定義
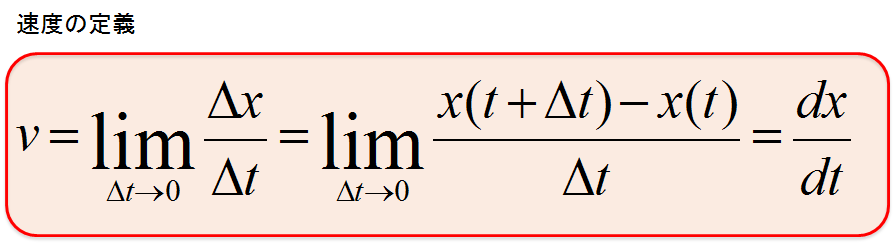
「速度の定義式を書け」と言われたら「$v=\frac{dx}{dt}$」と答えるのが正解です。(1次元の場合)
この式を、さらっと書きましたが、よく見ると導関数を求める式と同じ形をしていますね。
物理と微積は密接に関わっているのです。
微積の概念を使って物理の現象を表現することは非常に有効です。