2014.11.09掲載のリライト
鉛直投げ上げモデルと自由落下モデルの運動方程式は同じだった!
「えっ?」って思いましたか?
それとも「そんなの当たり前じゃん」と思いましたか?
それでは、鉛直投げ上げモデルを考えてみましょう。
質量$m$、初速度$v_0$で投げ上げたとします。
軸の設定
まずは軸の設定です。
上向きを正として
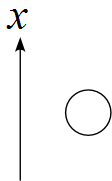
物体に作用する力を書く
次に力を書き込みます。
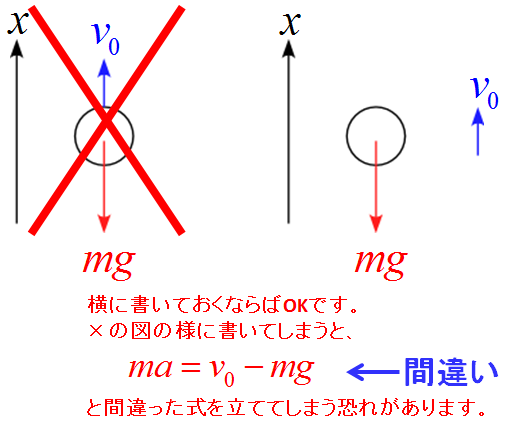
図に初速度$v_0$とか書き込んでいませんか?
間違いの元ですよ!
運動方程式を立てる
運動方程式は
\begin{eqnarray*}
ma=-mg
\end{eqnarray*}
となります。
はい、見たことありますね?
上を正に取った場合の自由落下の運動方程式と同じものです。
自由落下と鉛直投げ上げの違いは初速度$v_0$をつけるかどうかの差です。
どちらも物体に作用している力は重力のみであり、自由落下も鉛直投げ上げも同じです。
従って、運動方程式が同じになるのは当然のことになります。
初速度$v_0$は運動方程式を解いた時に出てくる積分定数を決定するときに必要になりますが、
運動方程式を立てることとは無関係です。
運動方程式を立てるために着目することは「力とその向き」です。
運動方程式を解く
さて、運動方程式を解いていきましょう。
\begin{eqnarray*}
ma &=& -mg \\
m\frac{dv}{dt} &=& -mg \\
\frac{dv}{dt} &=& -g
\end{eqnarray*}
これを解くことになります。
両辺$t$で積分すると、
\begin{eqnarray*}
\int \frac{dv}{dt} dt &=& -\int g\ dt \\
\int dv &=& - \int g\ dt\\
v &=& -gt+C
\end{eqnarray*}
となります。
ここで、初期条件の出番になります。
$t=0$のとき$v=v_0$なので、
\begin{eqnarray*}
v(0)=-g \cdot 0+C &=& v_0 \\
C &=& v_0
\end{eqnarray*}
\begin{eqnarray*}
v(t)=-gt+v_0 \\
\end{eqnarray*}
となり、さらに$t$で積分していくと
\begin{eqnarray*}
v(t)=\frac{dx}{dt} =- gt +v_0
\end{eqnarray*}
両辺を$t$で積分して
\begin{eqnarray*}
\int \frac{dx}{dt} dt &=& \int (-gt+v_0) \ dt\\
\int dx &=& \int (-gt +v_0 )\ dt\\
x &=& -\frac{1}{2}gt^2 + v_0 t +C'
\end{eqnarray*}
ここで$t=0$で原点とすれば
\begin{eqnarray*}
x(t) =- \frac{1}{2} g \cdot 0^2 +v_o \cdot 0 +C' &=& 0 \\
C' &=& 0
\end{eqnarray*}
よって
\begin{eqnarray*}
x(t) &=& -\frac{1}{2} gt^2 +v_0 t \\
\end{eqnarray*}
となるわけです。
教科書などで公式をして掲載されている式と同じになります。
グラフに表す
$v(t),\ x(t) \ $のグラフを考えてみましょう。
\begin{eqnarray*}
v(t)=-gt+v_0 \\
\end{eqnarray*}
であるから
$v(t)$はスタート時$v_0$で傾きが$-g$の直線になります。
最高点で$v=0$となり、その後下向きに落ちてきます。
\begin{eqnarray*}
x(t) &=& -\frac{1}{2} gt^2 +v_0 t \\
\end{eqnarray*}
$x(t)$は2次関数です。
2次関数の頂点が物体の最高点になります。
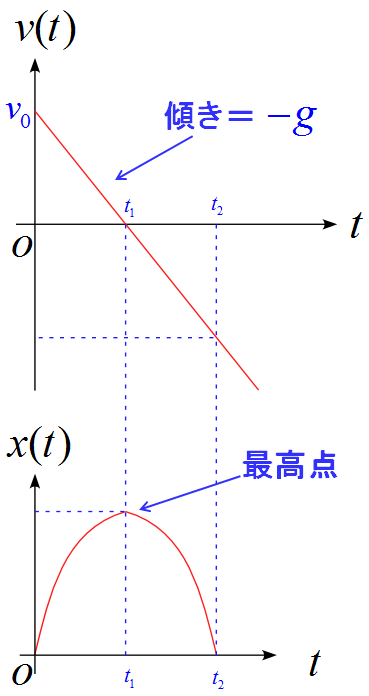
$v(t)=0$となるとき、時刻$t_1$とすると、$t_1$は
\begin{eqnarray*}
v(t_1) = -gt_1 +v_0 &= & 0 \\
t_1 & = & \frac{v_0}{g}
\end{eqnarray*}
となります。
この時、物体は最高点であり、その変位$x(t_1)$は
\begin{eqnarray*}
x(t_1) = x \Bigl( \frac{v_0}{g} \Bigr) & = &-\frac{1}{2} g \Bigl( \frac{v_0}{g} \Bigr) ^2 +v_0 \frac{v_0}{g} \\
&=& - \frac{1}{2}\frac{v_0^2}{g} +\frac{v_0^2}{g} \\
&=& \frac{v_0^2}{2g}
\end{eqnarray*}
となります。
その後物体は落下していき、元の位置に戻ったとき、
即ち、$x(t)$が$0$になる時を考えると
\begin{eqnarray*}
x(t) &=& -\frac{1}{2} gt^2 +v_0 t \\
&=& t\ \Bigl( -\frac{1}{2} gt +v_0 \Bigr)
\end{eqnarray*}
この式が$x(t)=0\ $となるのは$\ t=0\ $か$-\frac{1}{2} gt +v_0 =0\ $の時、
$t=0\ $はスタート時であり、$-\frac{1}{2} gt +v_0\ $は戻ってきた時であると考えられる。
戻った時の時刻を$t_2$とすると、
\begin{eqnarray*}
-\frac{1}{2} gt_2 +v_0 &=& 0\\
t_2 &=& \frac{2v_0}{g}
\end{eqnarray*}
となります。
よって、$t_2=2t_1$であり、行きと戻りにかかる時間は同じであるということがわかります。
戻って来た時の速度$v(t_2)$は
\begin{eqnarray*}
v(t_2) = v \Bigl( \frac{2v_0}{g} \Bigr) &=& -g \frac{2v_0}{g} +v_0 \\
&=& -2v_0 +v_0 \\
&=& -v_0
\end{eqnarray*}
となる。
これは初速度と大きさが同じで逆向きの速度になっています。
これらをグラフに表すと、
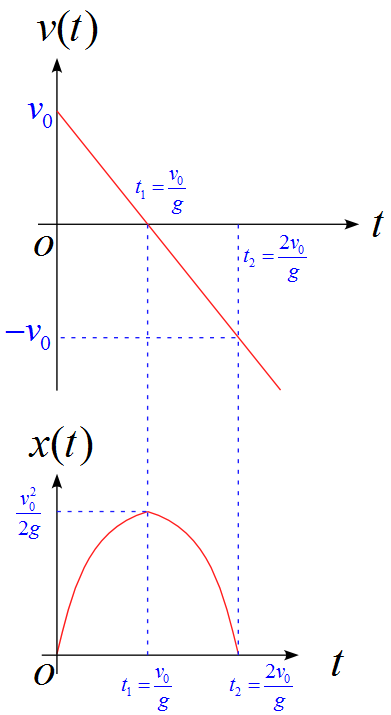
となります。